LeetCode 1155

leetcode_1155

LeetCode Contest 149 No.2

这里有 d 个一样的骰子，每个骰子上都有 f 个面，分别标号为 1, 2, ..., f。

我们约定：掷骰子的得到总点数为各骰子面朝上的数字的总和。

如果需要掷出的总点数为 target，请你计算出有多少种不同的组合情况（所有的组合情况总共有 f^d 种），模 10^9 + 7 后返回。

一开始我以为这是一道数学题，排列组合的数学题

因为上学的时候就是那样做的，只是有些特殊情况

然后我发现这道题的特殊情况数都数不完，我傻了

有那么一个瞬间我在想会不会是 DP ，似乎有点像

但是我不确定，随便想一下也没有想到 DP 怎么做

于是我就放弃这条思路去看 airpods 去了。。。。

竞赛结束之后我看了看别人的答案，只看了两秒钟

这不就是DP么，我关掉解答开始自己好好做这道题

开始：

class Solution:
def numRollsToTarget(self, d: int, f: int, target: int) -> int:
    MOD = 10**9 + 7
    nums = [[0]*target for _ in range(d)]
    for i in range(min(f,target)):
        nums[0][i] = 1
    for k in range(1,d):
        for i in range(1,target):
            nums[k][i] = sum(nums[k-1][max(0,i-f):i])
    return nums[-1][-1]%MOD

下面以5个骰子，每个骰子6个面，要求总和为16举例：

创建一个5*16的数组，横向代表骰子的点数总和，纵向代表骰子的数量，表格内的数字代表用x个骰子拼凑出y的点数总和，共有多少种情况

首先填写第一行的数据：用一个骰子扔出总和是 1、2、3、4、5、6 的情况均只有一种，用一个骰子扔出总和是7、8、9等的情况不存在

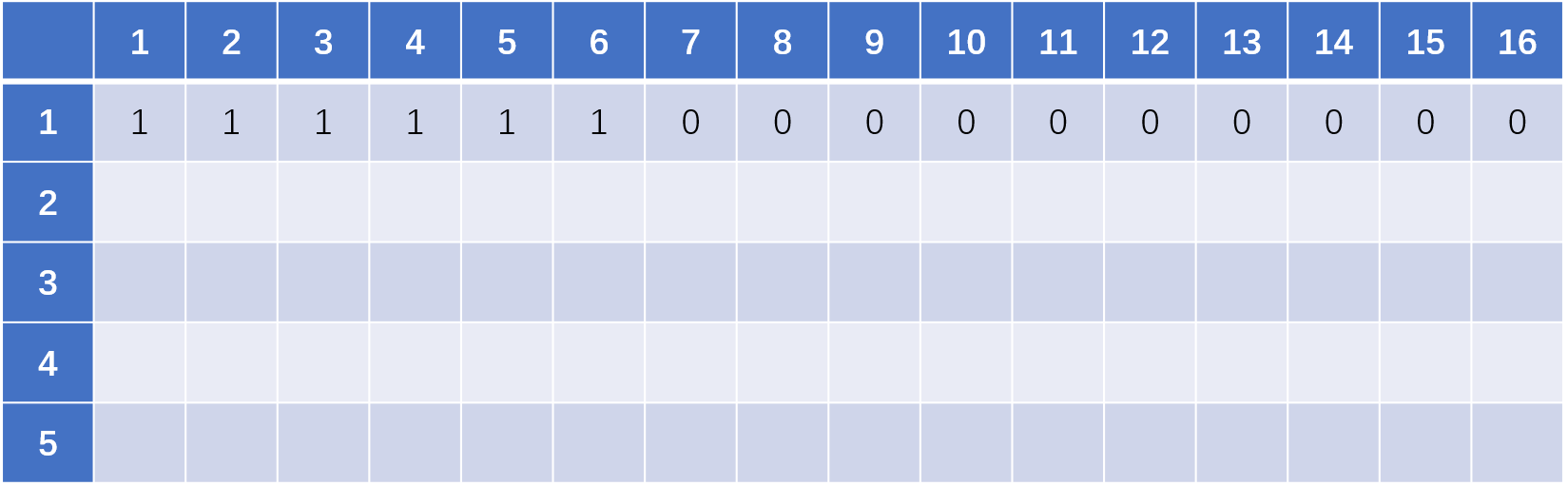
填写第二行的数据：

用两个骰子扔出总和是1的可能情况不存在
用两个骰子扔出总和是2的可能情况只有1种，是(1,1)
用两个骰子扔出总和是3的可能情况有两种，是(1,2)和(2,1)
依次类推

我们可以这样去考虑：第二个骰子可能扔出的情况是1、2、3、4、5、6六种情况，举例如果我们要填写第二行第八个空格，即要求扔出的总和为8，那么8的可能情况数量为以前的骰子扔出的情况为7、6、5、4、3、2这六种情况的总和。即，当第二个骰子扔出1时，以前的骰子总和为7，第二个骰子扔出2时，以前的骰子总和为6，依次类推

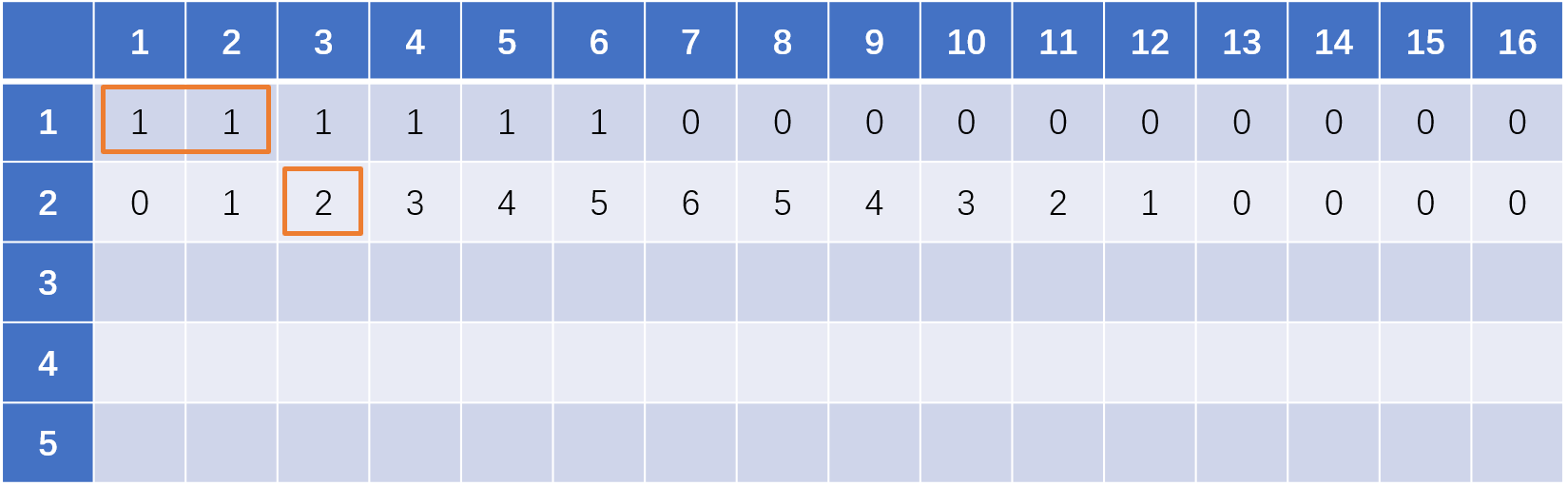
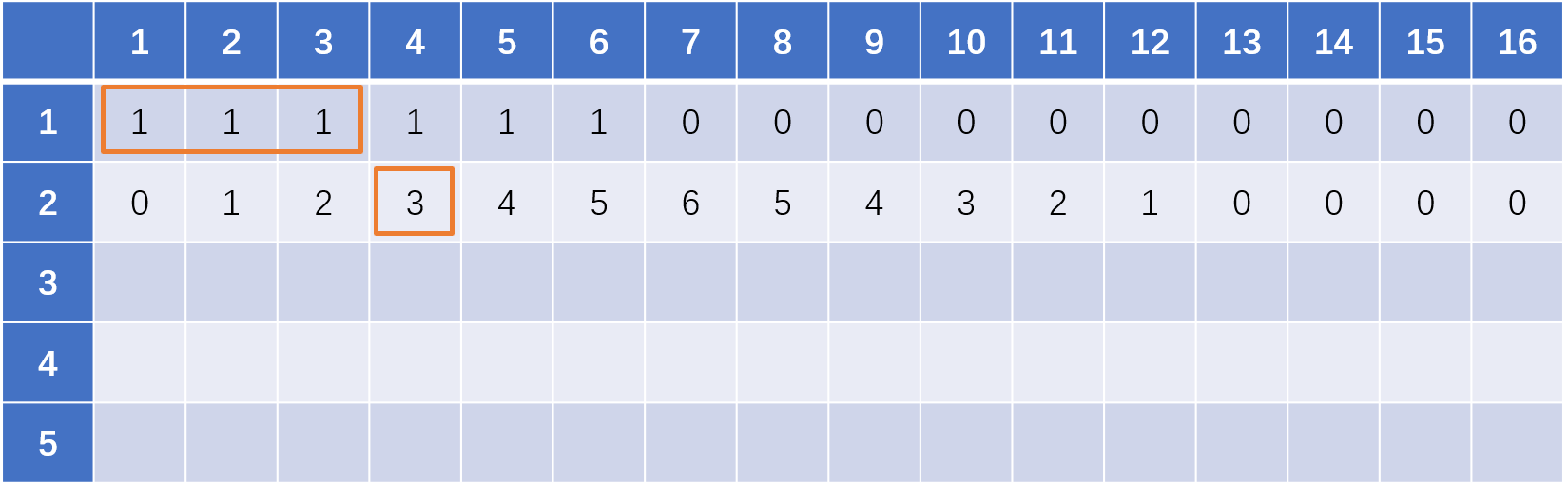
在表格中表示即为，某一格的值为在上一行不包括当前格子向左数六个格子的总和，即下图橙色框表示的区域

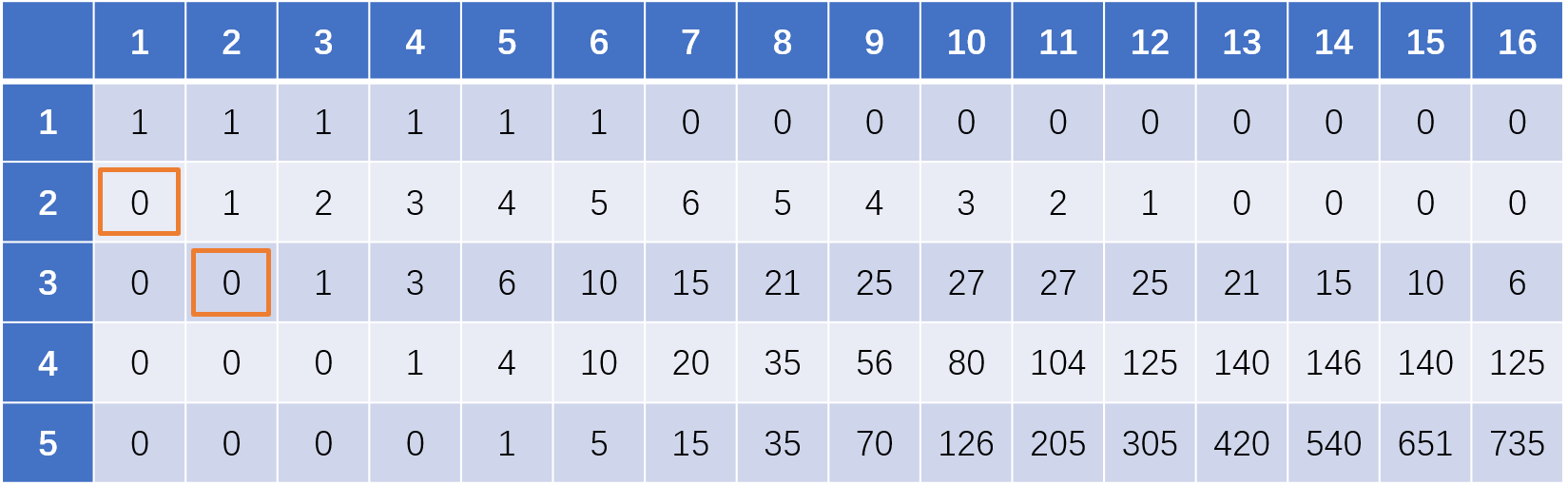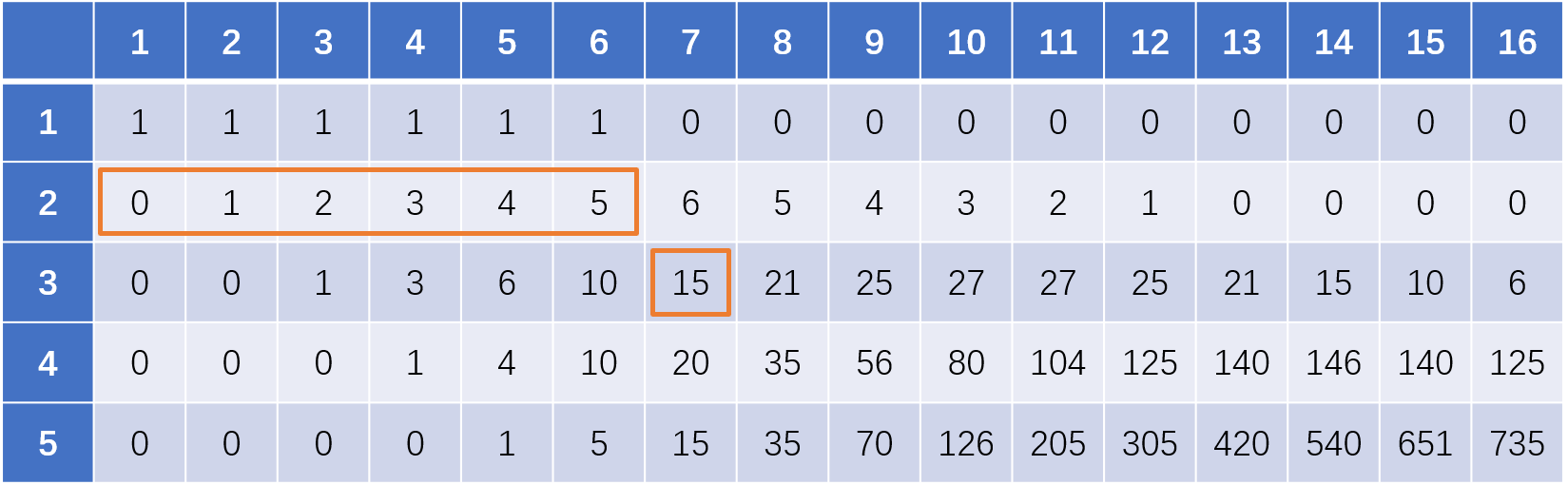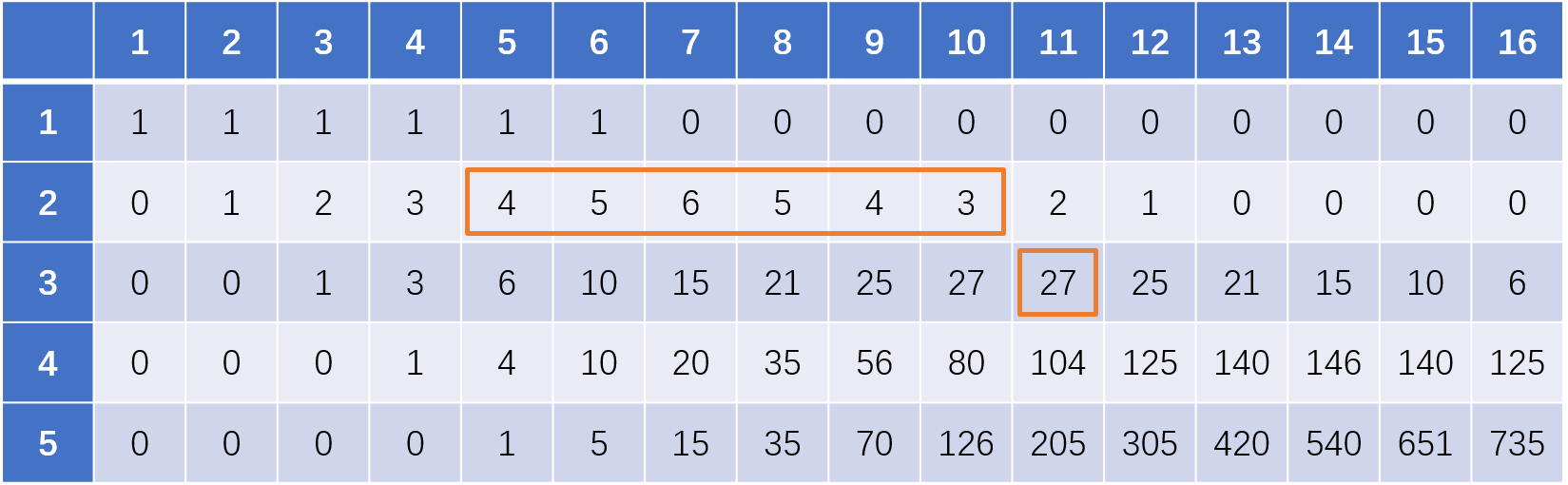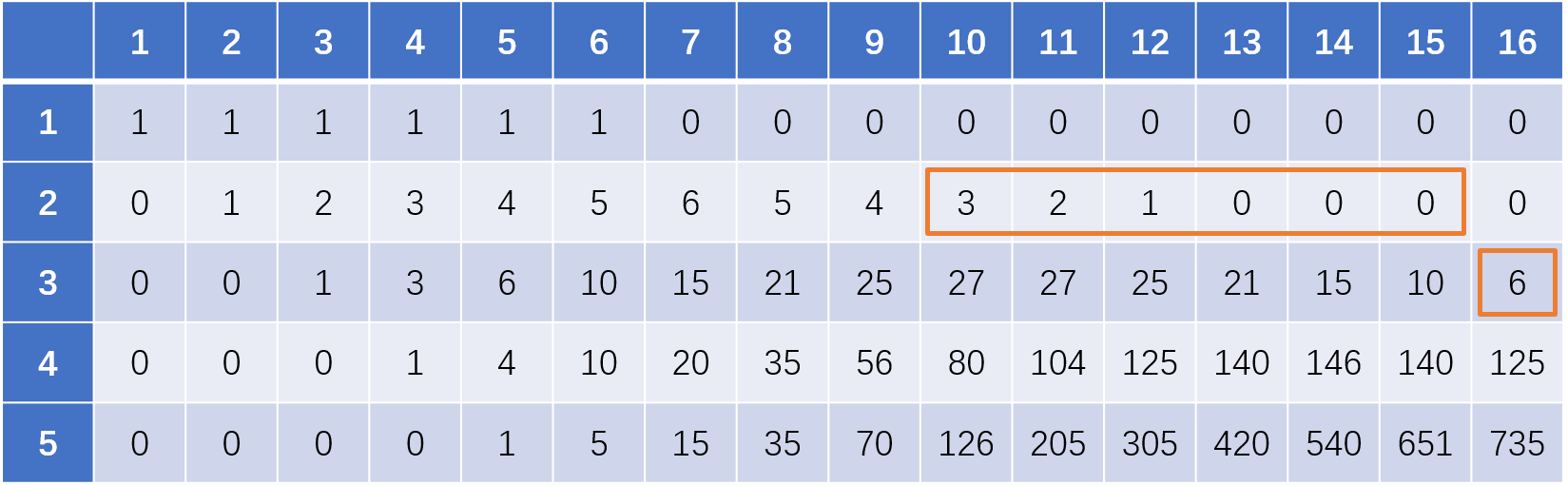
以此类推填写完整个表格

在本例中，表格右下角的数字即为5个骰子扔出总和为16的可能情况数量，为735

将本例拓宽到d个骰子f个面扔出总和为target的情况数量即为题目要求

下面重新看一下程序并将整个过程梳理一遍

class Solution:
def numRollsToTarget(self, d: int, f: int, target: int) -> int:
    MOD = 10**9 + 7
    nums = [[0]*target for _ in range(d)] # 初始化数组
    for i in range(min(f,target)):
        nums[0][i] = 1 # 填第一行的数
    for k in range(1,d):
        for i in range(1,target):
            nums[k][i] = sum(nums[k-1][max(0,i-f):i]) # 依次填写后面行的数
    return nums[-1][-1]%MOD #返回最终数的MOD值

建立一个二维矩阵，行数为d，列数为target，矩阵内容初始化为0
将第一行前f个数填为1
对于剩余的格子，每个格子等于上一行向前数f个数的和
返回矩阵的最后一个数

DONE